• ZŠ, ZŠ+, SŠ, VŠ
  Rovnoměrný přímočarý pohyb
• SŠ, VŠ
  Rovnoměrně zrychlený přímočarý pohyb
• SŠ, SŠ+, VŠ
  Rovnoměrný pohyb po kružnici I
• SŠ, SŠ+
  Rovnoměrný pohyb po kružnici II

• SŠ, SŠ+, VŠ
  Nepružné srážky těles
• SŠ, SŠ+, VŠ
  Pružné srážky těles

• SŠ, SŠ+, VŠ
  Matematické kyvadlo a tíhové zrychlení
• SŠ+, VŠ
  Matematické kyvadlo se zarážkou
• SŠ, SŠ+, VŠ
  Pružinový oscilátor a tuhost pružiny
• SŠ+, VŠ
  Pružinový oscilátor a spojování pružin

Pružinový oscilátor a spojování pružin

31. 3. 2012, 18:04

15. 12. 2012, 17:26

Zdeněk Pucholt

Cíl úlohy

Určit periodu vlastního kmitání složitějších pružinových oscilátorů – sériové a paralelní zapojení pružin. Ověřit vztah pro periodu vlastního kmitání.

Fyzikální princip

Pro periodu vlastního kmitání pružinového oscilátoru lze odvodit vztah

\begin{equation} T_0=2\pi\sqrt{\frac{m}{k}}\:\mbox{,}\label{eq:rce1} \end{equation}

který platí pro oscilátor složený z jedné pružiny a zavěšeného závaží. Vztah neplatí v případě využití dvou a více pružin sériově nebo paralelně zapojených.

Sériové zapojení pružin

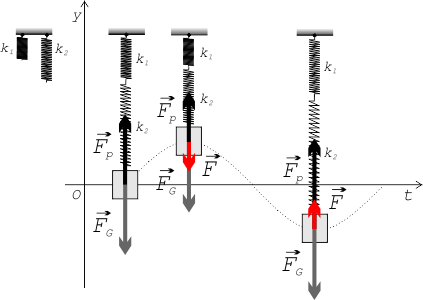
Sériově zapojené pružiny jsou v rovnovážné poloze zatíženy celou tíhou závaží $G$, platí proto

\begin{equation} k_1\Delta l_1=k_2\Delta l_2=G=mg\:\mbox{,}\label{eq:rce2} \end{equation}

kde $k_1$ a $k_2$ označují tuhosti pružin, $\Delta l_1$ a $\Delta l_2$ prodloužení pružin.

Při vychýlení závaží o vzdálenost $y$ směrem nahoru, se zkrátí první pružina o  $y_1$ a druhá pružina o  $y_2$. Obě přitom budou napínány stejnou silou o velikosti

\begin{equation} F_{\rm p}=k_1(\Delta l_1-y_1)=k_2(\Delta l_2-y_2)\:\mbox{.}\label{eq:rce3} \end{equation}

S využitím \eqref{eq:rce2} a \eqref{eq:rce3} lze pro velikost výsledné síly působící na závaží o hmotnosti $m$ psát

\begin{eqnarray} F&=&F_{\rm {p1}}-mg=k_1(\Delta l_1-y_1)-mg=k_1\Delta l_1-k_1y_1-mg=-k_1y_1\:\mbox{,}\label{eq:rce4}\\ F&=&F_{\rm {p2}}-mg=k_2(\Delta l_2-y_2)-mg=k_2\Delta l_2-k_2y_2-mg=-k_2y_2\:\mbox{.}\label{eq:rce5} \end{eqnarray}

Na základě \eqref{eq:rce3} při porovnání \eqref{eq:rce4} a \eqref{eq:rce5} platí

\begin{equation} F=-k_1y_1=-k_2y_2\:\mbox{.}\label{eq:rce6} \end{equation}

Jestliže uvážíme, že pro celkové vychýlení závaží platí $y=y_1+y_2$, můžeme pak celkovou výchylku závaží $y$ zapsat s využitím \eqref{eq:rce6} $y=-\frac{F}{k_1}-\frac{F}{k_2}=-F(\frac{1}{k_1}+\frac{1}{k_2})$, odkud pro velikost výsledné síly dostáváme

\begin{equation} F=-\frac{k_1k_2}{k_1+k_2}y\:\mbox{.}\label{eq:rce7} \end{equation}

Na základě II. Newtonova pohybového zákona platí pro sílu způsobující harmonický pohyb mechanického oscilátoru $F=-m\omega^2y$, pak dostáváme za využití \eqref{eq:rce7} a $\omega=\frac{2\pi}{T_0}$ vztah pro periodu oscilátoru

\begin{equation} T_0=2\pi\sqrt{\frac{m(k_1+k_2)}{k_1k_2}}\:\mbox{.}\label{eq:rce8} \end{equation}

Porovnáním \eqref{eq:rce1} a \eqref{eq:rce8} získáváme vztah pro tuhost pružiny $k$, která by nahradila dvě sériově zapojené pružiny o tuhostech $k_1$ a $k_2$

$$k=\frac{k_1k_2}{k_1+k_2}\:\mbox{.}$$

Platí tedy, že při sériovém zapojení pružin se sčítají převrácené hodnoty jejich tuhostí.

Paralelní zapojení pružin

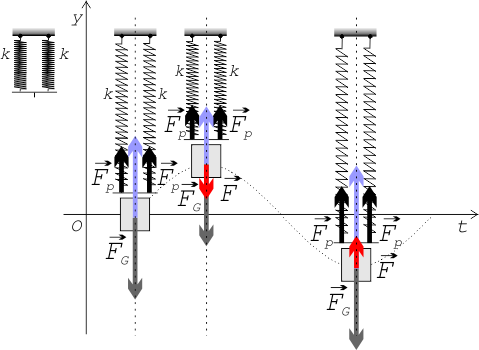
Oproti předchozímu zapojení se tíha závaží rozkládá na obě pružiny, platí proto v rovnovážné poloze

\begin{equation} k_1\Delta l_1+k_2\Delta l_2=mg\:\mbox{.}\label{eq:rce9} \end{equation}

Při vychýlení závaží o vzdálenost $y=y_1=y_2$ směrem nahoru, se síly pružnosti zmenší, potom platí pro velikost výsledné síly působící na závaží za využití \eqref{eq:rce9}

$$F=k_1(\Delta l_1-y)+k_2(\Delta l_2-y)-mg=-(k_1+k_2)y\:\mbox{.}$$

Podobně jako u předchozího případu dostáváme pro periodu oscilátoru

\begin{equation} T_0=2\pi\sqrt{\frac{m}{k_1+k_2}}\:\mbox{.}\label{eq:rce10} \end{equation}

Opětovným porovnáním s \eqref{eq:rce1} dostáváme vztah pro pružinu o tuhosti $k$, která by nahradila dvě paralelně zapojené pružiny o tuhostech $k_1$ a $k_2$

$$k=k_1+k_2\:\mbox{.}$$

Platí tedy, že při paralelním zapojení pružin se jejich tuhosti sčítají.

Poznámka: Pravidla pro výpočet celkové tuhosti soustavy pružin jsou analogická s výpočtem celkové kapacity soustavy kondenzátorů v elektrickém obvodu.

Videoanalýza

Vzhledem k poměrně přesnému měření času ve videoanalyzačním programu lze experimentálně stanovit doby kmitů oscilátorů a porovnat je s teoreticky vypočtenými hodnotami na základě vztahů \eqref{eq:rce8} a \eqref{eq:rce10}.

Pomůcky

Pružiny o různých tuhostech, závaží k zavěšení, stojan s držáky, propojovací tyč, kamera, software pro analýzu a zpracování videa.

Provedení

• Na laboratorní stojan umístíme kombinace pružin se závažím o hmotnosti $m=603\:\rm{g}$. Pokud umísťujeme dvě paralelně zapojené pružiny, využijeme k jejich propojení tyč o hmotnosti $m_{\rm t}=143\:\rm{g}$.
• Použijeme pružiny, jejichž tuhost předem známe. Pro pružinu s menším průměrem platí $k_1=26,6\:\rm{N\cdot m^{-1}}$, pro pružinu s větším průměrem pak $k_2=20,2\:\rm{N\cdot m^{-1}}$.
• Do videa umístíme vhodný předmět (pravítko), který využijeme jako kalibrační vzdálenost ve videu.
• Kameru umístíme tak, aby byl v záběru celý oscilátor. Dále provedeme vyrovnání kamery do vodorovného směru.
• Sériové zapojení stejných pružin: Využitím dvou stejných pružin o tuhostech $k_1$ se vztah \eqref{eq:rce8} zjednoduší na tvar \begin{equation} T_0=2\pi\sqrt{\frac{2m}{k_1}}\:\mbox{.}\label{eq:rce11} \end{equation}
• Sériové zapojení odlišných pružin: Stačí pouze využít vztah \eqref{eq:rce8}.
• Paralelní zapojení stejných pružin: Při paralelním zapojení je nutné využití propojovací tyče o hmotnosti $m_{\rm t}$. Využitím dvou stejných pružin o tuhostech $k_1$ se vztah \eqref{eq:rce10} zjednoduší na tvar \begin{equation} T_0=2\pi\sqrt{\frac{m+m_{\rm t}}{2k_1}}\:\mbox{.}\label{eq:rce12} \end{equation}
• U každého případu je výstupem graf závislosti y-souřadnice na čase $y(t)$.
  Pružinový oscilátor – spojování pružin.

Vyhodnocení

• Pomocí videoanalýzy lze poměrně přesně stanovit velikost periody jednotlivých oscilátorů.
• Sériové zapojení stejných pružin: Na základě \eqref{eq:rce11} dostáváme teoretickou hodnotu periody $T_{\rm t}=1,37\:\rm{s}$, pomocí videoanalýzy byla naměřena hodnota $T=1,36\:\rm{s}$.
• Sériové zapojení odlišných pružin: Dosazením do vztahu \eqref{eq:rce8} dostáváme teoretickou hodnotu periody $T_{\rm t}=1,44\:\rm{s}$, pomocí videoanalýzy byla naměřena hodnota $T=1,44\:\rm{s}$.
• Paralelní zapojení stejných pružin: Dosazením do vztahu \eqref{eq:rce12} dostáváme teoretickou hodnotu periody $T_{\rm t}=0,77\:\rm{s}$, pomocí videoanalýzy byla naměřena hodnota $T=0,76\:\rm{s}$.
• Lze tedy říci, že videoanalýza umožňuje poměrně přesně stanovit periodu pružinového oscilátoru, kterou lze využít i k dynamickému určování výsledné tuhosti zapojených pružin.

Použitá literatura a zdroje

• LEPIL, Oldřich. Fyzika pro gymnázia: Mechanické kmitání a vlnění. 3. přeprac. vyd. Praha: Prometheus, 2001, 129 s. ISBN 80-719-6216-3.
• ŠEDIVÝ, Přemysl, Ivo VOLF a Radmila Horáková. Harmonické kmity mechanických soustav: Studijní text pro řešitele FO a ostatní zájemce o fyziku. Dostupné z: http://fyzikalniolympiada.cz/texty/kmity.pdf.