• ZŠ, ZŠ+, SŠ, VŠ
  Rovnoměrný přímočarý pohyb
• SŠ, VŠ
  Rovnoměrně zrychlený přímočarý pohyb
• SŠ, SŠ+, VŠ
  Rovnoměrný pohyb po kružnici I
• SŠ, SŠ+
  Rovnoměrný pohyb po kružnici II

• SŠ, SŠ+, VŠ
  Nepružné srážky těles
• SŠ, SŠ+, VŠ
  Pružné srážky těles

• SŠ, SŠ+, VŠ
  Matematické kyvadlo a tíhové zrychlení
• SŠ+, VŠ
  Matematické kyvadlo se zarážkou
• SŠ, SŠ+, VŠ
  Pružinový oscilátor a tuhost pružiny
• SŠ+, VŠ
  Pružinový oscilátor a spojování pružin

Matematické kyvadlo a tíhové zrychlení

23. 3. 2012, 14:49

15. 12. 2012, 17:26

Zdeněk Pucholt

Cíl úlohy

Určit velikost místního tíhového zrychlení z doby kmitu.

Fyzikální princip

Kyvadlo zaujímá ve vývoji lidstva významou roli. V dřívějších dobách se využívalo pro měření času v kyvadlových hodinách. Obecně lze kyvadlo charakterizovat jako těleso zavěšené nad svým těžištěm, které se může volně otáčet kolem vodorovné osy procházející bodem závěsu kolmo k rovině kmitání.

V dalším se omezíme pouze na tzv. matematické kyvadlo, které je tvořeno hmotným bodem (v praxi nejčastěji malou kuličkou) upevněným na závěsu zanedbatelné hmotnosti a konstantní délky $l$.

Příčinou kmitavého pohybu kyvadla je existence vratné síly $\vec{F}$, která má tendenci jej při vychýlení z rovnovážné polohy vrátit zpět. Tato síla je výslednicí tíhové síly $\vec{F}_{\rm G}$ a tažné síly vlákna.

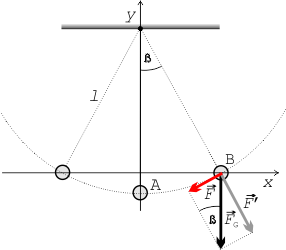
Je-li úhel $\beta$ malý, lze vzdálenost vychýleného hmotného bodu od počátku nahradit úsečkou, pak na základě podobnosti trojúhelníků platí

\begin{equation} \sin\beta\approx\beta\approx\frac{F}{F_{\rm G}}=\frac{x}{l}\:\mbox{.}\label{eq:rce1} \end{equation}

Jestliže pro sílu $\vec{F}$ způsobující harmonické kmitání podle II. Newtonova zákona platí $F=-m\omega^2x$, lze tuto sílu vyjádřit za využití \eqref{eq:rce1}

$$F=-m\omega^2x=-m\frac{g}{l}x\:\mbox{,}$$

odkud porovnáním dostáváme vztah pro úhlovou frekvenci $\omega_0$ vlastního kmitání

\begin{equation} \omega_0=\sqrt{\frac{g}{l}}\:\mbox{.}\label{eq:rce2} \end{equation}

Jestliže $\omega_0=\frac{2\pi}{T_0}$ , kde $T_0$ je perioda vlastního kmitání, s přihlédnutím ke \eqref{eq:rce3} platí

\begin{equation} T_0=2\pi\sqrt{\frac{g}{l}}\:\mbox{.}\label{eq:rce3} \end{equation}

Ze \eqref{eq:rce3} je patrné, že perioda kyvadla nezávisí na jeho hmotnosti ani na výchylce z rovnovážné polohy. Velikost tíhového zrychlení je konstantní, tedy jediný parametr ovlivňující periodu kyvadla je jeho délka – vzdálenost od bodu závěsu k těžišti kuličky.

Poznámka: V souvislosti s kyvadlem se využívá dalšího pojmu – kyv, který odpovídá polovině periody

$$\tau=\frac{T}{2}\:\mbox{.}$$

Videoanalýza

Velikost a směr tíhové síly jsou během celé doby pohybu kyvadla stejné, naopak velikost a směr tahové síly lana se mění. Podle obrázku lze pro velikost vratné síly psát

$$F=mg\sin\beta\:\mbox{.}$$

Jelikož je velikost tíhového zrychlení $g$ ovlivněna zeměpisnou šířkou, je vhodné si jeho velikost orientačně změřit. Pro jednoduché měření lze využít kuličky zavěšené na niti o známé délce $l$. Pro samotný výpočet lze vyjít ze vztahu \eqref{eq:rce3}, odkud pro velikost tíhového zrychlení platí

\begin{equation} g=4\pi^2\frac{l}{T^2}\:\mbox{.}\label{eq:rce4} \end{equation}

Pro porovnání získané hodnoty místního tíhového zrychlení z videoanalýzy se nabízí jeho určení na základě znalosti zeměpisné šířky. Lze vyjít z Lit.2, kde pro $g$ platí vztah

\begin{equation} g=9,78031846\:(1+0,005278895\sin^{2}(\varphi)+0,000023462\sin^{4}(\varphi))\:\rm{m\cdot s^{-2}}\label{eq:rce5} \end{equation}

pro danou zeměpisnou šířku $\varphi$. Vliv nadmořské výšky se projeví až na třetím desetinném místě, tudíž v rámci naší přesnosti není podstatný.

Pomůcky

Kulička s háčkem, nit, nůžky, závěs na zdi pro zavěšení matematického kyvadla, kamera, software pro analýzu a zpracování videa.

Provedení

• Před samotným analyzováním je zapotřebí provést změření průměru použité kuličky, v našem případě $d=25,3\:\rm{mm}$. Velikost průměru kuličky lze využít jako kalibrační vzdálenost ve videu.
• Kameru umístíme tak, aby v záběru bylo celé kyvadlo – od bodu závěsu po kuličku, pod kterou by mělo býti místo pro pozdější zakreslení vektorů. Dále provedeme vyrovnání kamery do vodorovného směru.
• Pomocí analyzačního programu určíme délku závěsu kyvadla (vzdálenost bodu uchycení závěsu – těžiště kuličky), v našem případě $l=1,002\:\rm{m}$.
• Aplikací filtrů lze docílit záměrného zanechávání stopy pohybu kuličky kyvadla.
• Do videa lze zakreslit působící síly a jejich výslednice v několika okamžicích a porovnat je, např. při maximální a nulové výchylce kyvadla.
• Pomocí videoanalýzy lze i stanovit velikost periody a dosadit do \eqref{eq:rce4} pro určení velikosti tíhového zrychlení.
• Výstupem videoanalýzy je komplexní video obsahující zakreslení vektorů působících sil ve vybraných bodech a grafy závislostí x-souřadnice na čase $x(t)$ a rychlosti na čase $v_{\rm x}(t)$.
  Matematické kyvadlo – charakteristika kyvadla.

Vyhodnocení

• Z videa je patrné, že kulička, resp. kyvadlo, koná harmonický pohyb, jehož příčinou je existence vratné síly, která má tendenci jej vrátit zpět do rovnovážné polohy. Do videa byla zakreslena stopa pohybu kuličky včetně sil působících ve vybraných bodech trajektorie kuličky.
• Videoanalýzou lze poměrně přesně stanovit periodu kyvadla, což umožňuje určit velikost tíhového zrychlení v daném místě. Původní nastavená metrová délka kyvadla se změnila vlivem tíhy kuličky a háčku, závěs se tak prodloužil na své délce o  $\Delta l=2\:\rm{mm}$. Z videa lze odečíst dobu jedné periody kyvadla, v našem případě $T=2,01\:\rm{s}\:\mbox{,}$ z čehož po dosazení do \eqref{eq:rce4} dostáváme pro velikost tíhového zrychlení $g\approx 9,79\:\rm{m\cdot s^{-2}}$.
• Jestliže uvážíme, že budova PřF v Olomouci, kde měření probíhalo, leží na $49,59^\circ$ s. š. (ověřeno GPS senzorem Vernier), kde hodnota tíhového zrychlení podle \eqref{eq:rce5} odpovídá $g^{'}\approx 9,81\:\rm{m\cdot s^{-2}}$, můžeme považovat naše měření v rámci naší přesnosti za úspěšné, jelikož relativní chyba měření $\delta_{\rm{g}}=0,2\,%$.
• Výstupem videoanalýzy jsou rovněž grafy zobrazující časové závislosti vybraných veličin. Z níže uvedených grafů jasně vyplývá, že v případě průchodu kyvadla rovnovážnou polohou je hodnota x-ové souřadnice nulová, hodnota rychlosti $v_{\rm x}$ největší a hodnota zrychlení $a_{\rm x}$ nulová. V krajních bodech, kde je úhlová výchylka $\Theta_{\rm r}$ největší, má kyvadlo nejmenší (nulovou) rychlost a největší zrychlení. Během pohybu se mění směry rychlosti i zrychlení.
  

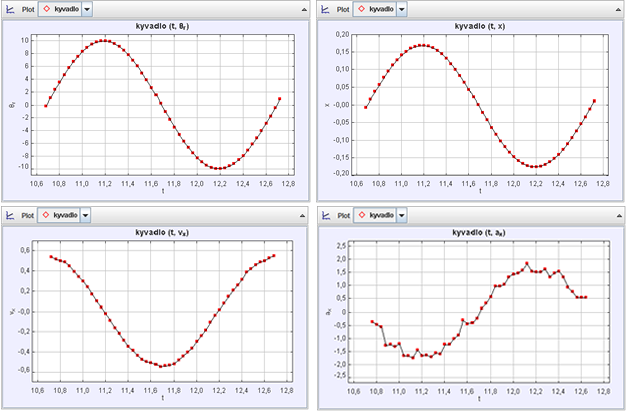  Nahoře vlevo – graf časové závislosti úhlové výchylky kyvadla, nahoře vpravo – graf časové závislosti x-ové souřadnice, dole vlevo – graf časové závislosti rychlosti, dole vpravo – graf časové závislosti zrychlení.
  

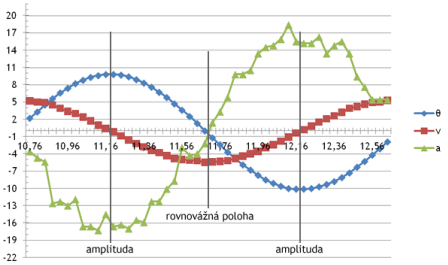  Souvislost vybraných veličin v několika typických polohách matematického kyvadla – rovnovážná poloha, amplitudy.

Použitá literatura a zdroje

• LEPIL, Oldřich. Fyzika pro gymnázia: mechanické kmitání a vlnění. 3. přeprac. vyd. Praha: Prometheus, 2001, 129 s. ISBN 80-719-6216-3.
• TELFORD, W. Applied geophysics. 2nd ed. Cambridge: Cambridge University Press, 1990, 770 s. ISBN 05-213-3938-3.
• Vzdáleně ovládaná laboratoř: Určení tíhového zrychlení z doby kmitu matematického kyvadla. Dostupné z: http://ictphysics.upol.cz/remotelab/rlab2_sestava.html.