• ZŠ, ZŠ+, SŠ, VŠ
  Rovnoměrný přímočarý pohyb
• SŠ, VŠ
  Rovnoměrně zrychlený přímočarý pohyb
• SŠ, SŠ+, VŠ
  Rovnoměrný pohyb po kružnici I
• SŠ, SŠ+
  Rovnoměrný pohyb po kružnici II

• SŠ, SŠ+, VŠ
  Nepružné srážky těles
• SŠ, SŠ+, VŠ
  Pružné srážky těles

• SŠ, SŠ+, VŠ
  Matematické kyvadlo a tíhové zrychlení
• SŠ+, VŠ
  Matematické kyvadlo se zarážkou
• SŠ, SŠ+, VŠ
  Pružinový oscilátor a tuhost pružiny
• SŠ+, VŠ
  Pružinový oscilátor a spojování pružin

Pružné srážky těles

19. 3. 2012, 20:45

15. 12. 2012, 17:26

Zdeněk Pucholt

Cíl úlohy

Určit rychlosti vozíků po pružné srážce.

Fyzikální princip

Vlivem vnějších sil tělesa plynule mění svoji rychlost a směr pohybu podle pohybových zákonů. V některých případech dochází k omezení pohybu tělesa, jelikož se v jeho směru pohybu nacházejí jiná tělesa – dochází ke srážce.

Během srážky se mění směr a rychlost pohybu těles téměř skokem vlivem přítomnosti nárazových sil. V případě srážky pružných pevných těles (např. ocelové součásti) se taková srážka označuje jako rázy těles.

Pokud při srážce platí zákon zachování kinetické energie, jde o srážku pružnou, pokud neplatí, jde o srážku nepružnou. Pokud při srážce nedojde k žádnému odpružení těles a tyto se dále pohybují jako jedno těleso, jde o srážku dokonale nepružnou, při částečném odpružení jde o srážku nedokonale pružnou. Jestliže těleso narazí na nepropustnou stěnu, označujeme takovou srážku jako odraz tělesa.

Dokonale pružná srážka

Uvažujme dvě dokonale pružné koule o hmotnostech $m_{\rm 1}$ a $m_{\rm 2}$, které se pohybují rovnoměrně přímočaře, přímo proti sobě – nastane přímá srážka. Kladnou orientaci rychlosti přisoudíme pohybu zleva doprava.

Při srážce se dočasně obě koule deformují, ale během okamžiku se jejich deformační energie přemění zpět na kinetickou energii – obě koule se od sebe pružně odrazí, nastává dokonale pružná srážka.

Je zřejmé, že se při této srážce zachovává celková hybnost soustavy a také celková energie. Platí zákon zachování hybnosti

\begin{equation} m_{\rm 1}v_{\rm 1}+m_{\rm 2}v_{\rm 2}=m_{\rm 1}v^{'}_{\rm 1}+m_{\rm 2}v^{'}_{\rm 2}\:\mbox{,}\label{eq:rce1} \end{equation}

zákon zachování mechanické energie

\begin{equation} \frac{1}{2}m_{\rm 1}v^2_{\rm 1}+\frac{1}{2}m_{\rm 2}v^2_{\rm 2}=\frac{1}{2}m_{\rm 1}v^{'2}_{\rm 1}+\frac{1}{2}m_{\rm 2}v^{'2}_{\rm 2}\:\mbox{.}\label{eq:rce2} \end{equation}

Obecným řešením soustavy rovnic \eqref{eq:rce1} a \eqref{eq:rce2} pro $v^{'}_{\rm 1}$, $v^{'}_{\rm 2}$ je

\begin{equation} v^{'}_{\rm 1}=v_{\rm 1}\frac{m_{\rm 1}-m_{\rm 2}}{m_{\rm 1}+m_{\rm 2}}+v_{\rm 2}\frac{2m_{\rm 2}}{m_{\rm 1}+m_{\rm 2}}\:\mbox{,}\label{eq:rce3} \end{equation} \begin{equation} v^{'}_{\rm 2}=v_{\rm 1}\frac{2m_{\rm 1}}{m_{\rm 1}+m_{\rm 2}}-v_{\rm 2}\frac{m_{\rm 1}-m_{\rm 2}}{m_{\rm 1}+m_{\rm 2}}\:\mbox{.}\label{eq:rce4} \end{equation}

Jestliže mají obě koule stejné hmotnosti $m_{\rm 1}=m_{\rm 2}$, dostáváme jednodušší tvar řešení soustavy rovnic \eqref{eq:rce1} a \eqref{eq:rce2}

\begin{equation} v^{'}_{\rm 1}=v_{\rm 2}\:\mbox{,}\label{eq:rce5} \end{equation} \begin{equation} v^{'}_{\rm 2}=v_{\rm 1}\:\mbox{.}\label{eq:rce6} \end{equation}

Lze tedy říci, že v případě pružné čelní srážky dvou stejných koulí si obě koule navzájem vymění své rychlosti. Tento poznatek se využívá u srážkostrojů (rázostrojů), kde si stejné kuličky vyměňují svoje rychlosti.

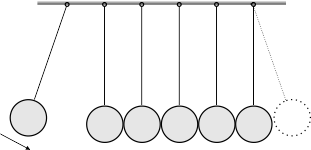
Videoanalýza

Pružnou srážku můžeme velmi jednoduše realizovat na vozíčkové dráze, za použití dvou vozíků, na jejichž koncích jsou pružiny.

Pomůcky

Vozíčková dráha s příslušenstvím, kamera, barevná lepící páska, vhodné měřidlo, software pro analýzu a zpracování videa.

Provedení

• Při realizaci je vhodné zaměřit se na vybrané situace. Uvažujme vozík s hmotností $m^{'}_{\rm 1}$, kterému je na počátku udělen krátký silový impuls, takže se dále pohybuje rovnoměrným přímočarým pohybem rychlostí $v_{\rm 1}$. Tento vozík narazí do dalšího vozíku o hmotnosti $m^{'}_{\rm 2}$, který je vždy v klidu, tzn. $v_{\rm 2}=0\:\rm{m\cdot s^{-1}}$.
• Jestliže některý z vozíků zatížíme (uvažujme vždy stejná závaží), přidáme vždy dvě závaží (na každou stranu vozíku jedno). Pro vozík s hmotností $m^{'}_{\rm 1}$ bude platit \begin{equation} m_{\rm 1}=m^{'}_{\rm 1}+2nm_{\rm z}\mbox{,}\label{eq:rce7} \end{equation} kde $n$ odpovídá počtu zatížení, $m_{\rm z}$ hmotnosti jednoho závaží. Pro 2-krát zatížený vozík tak dostáváme $m_{\rm 1}=m^{'}_{\rm 1}+4m_{\rm z}$, podobně pro druhý vozík definujeme celkovou hmotnost jako $$m_{\rm 2}=m^{'}_{\rm 2}+2nm_{\rm z}\mbox{.}$$ V případě, že máme k dispozici dva identické vozíky, platí $m^{'}=m^{'}_{\rm 1}=m^{'}_{\rm 2}$.
• Nezatížené vozíky, stejně zatížené vozíky: Tuto situaci popisují rovnice \eqref{eq:rce5} a \eqref{eq:rce6}. Je zřejmé, že v tomto případě si vozíky navzájem vymění své rychlosti.
• První vozík zatížen čtyřmi závažími: První vozík jsme tedy podle \eqref{eq:rce7} dvakrát zatížili, druhý vozík zůstal nezatížen. Rovnice \eqref{eq:rce3} a \eqref{eq:rce4} budou ve tvaru \begin{eqnarray} v^{'}_{\rm 1} &=& \frac{2v_{\rm 1}m_{\rm z}}{2m_{\rm z}+m^{'}}\:\mbox{,}\label{eq:rce8}\nonumber\\ v^{'}_{\rm 2} &=& \frac{v_{\rm 1}(m^{'}+4m_{\rm z})}{2m_{\rm z}+m^{'}}\:\mbox{.} \end{eqnarray}
• Druhý vozík zatížen čtyřmi závažími: Oproti předchozímu dojde pouze k výměně závaží mezi vozíky, druhý vozík tak bude dvakrát zatížen, první zůstane nezatížen. Dostáváme pak \begin{eqnarray} v^{'}_{\rm 1} &=& -\frac{2v_{\rm 1}m_{\rm z}}{2m_{\rm z}+m^{'}}\:\mbox{,}\label{eq:rce9}\nonumber\\ v^{'}_{\rm 2} &=& \frac{m^{'}v_{\rm 1}}{2m_{\rm z}+m^{'}}\:\mbox{.} \end{eqnarray} Je zřejmé, že směr rychlosti $v^{'}_{\rm 1}$ je opačný, než původní směr vozíku, vozík se tak bude pohybovat zpět.
• Sestavíme vozíčkovou dráhu. Je nutné ji před začátkem měření vyvážit tak, aby se při vhánění vzduchu z kompresoru do dráhy volně položené vozíky nepohybovaly.
• Provedeme změření a zvážení kalibračního předmětu – např. pro délku a hmotnost obou vozíků platí $l=12,5\:\rm cm$, $m^{'}=76,6\:\rm g$. Délka vozíku $l$ je zakreslena i v analyzovaném videu.
• Použité závaží k zatížení vozíku má hmotnost $m_{\rm z}=49,5\:\rm g$.
• Vozíky vhodně označíme barevnou páskou – usnadní nám to realizaci videoanalýzy.
• Kameru pro snímání umístíme tak, aby byla v záběru celá vozíčková dráha. Dále provedeme vyrovnání kamery do vodorovného směru.
• Získaný výstup ze snímací kamery zpracujeme ve vhodném analyzačním softwaru.

Vyhodnocení

• Nezatížené vozíky: V tomto případě nás zajímá pouze velikost průměrné rychlosti $v_{\rm 1}$ a velikost průměrné rychlosti $v^{'}_{\rm 2}$. Z videoanalýzy lze určit $v_{\rm 1}=0,68\:\rm{m\cdot s^{-1}}$, $v^{'}_{\rm 2}=0,60\:\rm{m\cdot s^{-1}}$. Je tedy patrné, že druhý vozík převzal rychlost od prvního vozíku, který se na místě srážky zastavil.
• Stejně zatížené vozíky: Na základě předchozích úvah budeme opět zjišťovat velikosti průměrných rychlostí $v_{\rm 1}$ a $v^{'}_{\rm 2}$. Získáváme $v_{\rm 1}=0,51\:\rm{m\cdot s^{-1}}$, $v^{'}_{\rm 2}=0,48\:\rm{m\cdot s^{-1}}$. V tomto případě získáváme přesnější hodnoty, z důvodu větší míry setrvačnosti vozíků. Tato skutečnost se potvrzuje i u jiných experimentů prováděných na vozíčkové dráze.
• První vozík zatížen čtyřmi závažími: Podle vztahů \eqref{eq:rce8} a znalosti průměrné rychlosti $v_{\rm 1}$ lze určit rychlosti $v^{'}_{\rm 1}$ a $v^{'}_{\rm 2}$. První vozík se již bude po srážce také pohybovat, stejně jako druhý vozík. Z videoanalýzy lze získat pro $v_{\rm 1}=0,52\:\rm{m\cdot s^{-1}}$, $v^{'}_{\rm 1}=0,27\:\rm{m\cdot s^{-1}}$ a $v^{'}_{\rm 2}=0,73\:\rm{m\cdot s^{-1}}$. Při porovnání s teoretickými hodnotami dostáváme pro rychlost $v^{'}_{\rm 1}$ rychlostní rozdíl $\Delta v^{'}_{\rm 1}=|v^{'}_{\rm {t1}}-v^{'}_{\rm 1}|=0,02\:\rm{m\cdot s^{-1}}$, kde $v^{'}_{\rm {t1}}$ označuje teoreticky vypočtenou rychlost pohybu prvního vozíku po srážce z  $v_{\rm 1}$. Podobně pro rychlost $v^{'}_{\rm 2}$ máme rychlostní rozdíl $\Delta v^{'}_{\rm 2}=|v^{'}_{\rm {t2}}-v^{'}_{\rm 2}|=0,08\:\rm{m\cdot s^{-1}}$.
• Druhý vozík zatížen čtyřmi závažími: Při pohledu na rovnice \eqref{eq:rce9} je jasné, že se první vozík bude po srážce vracet zpět. Z provedené videoanalýzy lze zjistit hodnoty průměrných rychlostí $v_{\rm 1}=0,80\:\rm{m\cdot s^{-1}}$, $v^{'}_{\rm 1}=-0,41\:\rm{m\cdot s^{-1}}$ a $v^{'}_{\rm 2}=0,34\:\rm{m\cdot s^{-1}}$. Rychlostní rozdíly pro rychlosti $v^{'}_{\rm 1}$ a $v^{'}_{\rm 2}$ jsou $\Delta v^{'}_{\rm 1}=|v^{'}_{\rm {t1}}-v^{'}_{\rm 1}|=0,04\:\rm{m\cdot s^{-1}}$, $\Delta v^{'}_{\rm 2}=|v^{'}_{\rm {t2}}-v^{'}_{\rm 2}|=0,01\:\rm{m\cdot s^{-1}}$.

Použitá literatura a zdroje

• BAJER, Jiří. Mechanika 2. 1. vyd. Olomouc: Univerzita Palackého, 2004, 457 s. ISBN 80-244-0884-8.