| nepřihlášený uživatel (pouze prohlížení) |
| přihlásit | registrace |
-
ZŠ, ZŠ+, SŠ, VŠ
Rovnoměrný přímočarý pohyb -
SŠ, VŠ
Rovnoměrně zrychlený přímočarý pohyb -
SŠ, SŠ+, VŠ
Rovnoměrný pohyb po kružnici I -
SŠ, SŠ+
Rovnoměrný pohyb po kružnici II
-
SŠ, SŠ+, VŠ
Nepružné srážky těles -
SŠ, SŠ+, VŠ
Pružné srážky těles
-
SŠ, SŠ+, VŠ
Matematické kyvadlo a tíhové zrychlení -
SŠ+, VŠ
Matematické kyvadlo se zarážkou -
SŠ, SŠ+, VŠ
Pružinový oscilátor a tuhost pružiny -
SŠ+, VŠ
Pružinový oscilátor a spojování pružin
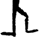
si můžete zobrazit video z příslušného videopokusu na celou obrazovku?
Rovnoměrný pohyb po kružnici I
Střední škola
Střední škola, pokročilí
Vysoká škola
 |
19. 4. 2012, 14:50 |  |
15. 12. 2012, 17:26 |  |
Zdeněk Pucholt |
Cíl úlohy
Analyzovat rovnoměrný pohyb po kružnici. Určit směr okamžité rychlosti a zrychlení.
Fyzikální princip
Trajektorie mechanických pohybů mají různé tvary – pohyby tak můžeme na základě tvaru trajektorie rozdělit do dvou hlavních skupin – přímočaré a křivočaré. Právě mezi křivočaré pohyby lze zařadit pohyb po kružnici.
Množství těles, která takový pohyb konají, je kolem nás mnoho – kulička na provázku, body brusného kotouče, body na gramofonové desce (CD nosiči), body na povrchu Země aj.
Rovnoměrný pohyb po kružnici je nejjednodušší křivočarý pohyb. Trajektorií hmotného bodu je kružnice, velikost rychlosti je během celého pohybu konstantní, ovšem její směr se neustále mění – v každém bodě trajektorie má směr tečny. V dalším budeme uvažovat právě tento typ pohybu.
Popisujeme-li pohyb vzhledem ke středu trajektorie, je poloha bodu určena průvodičem $\vec{r}$, jehož délka odpovídá poloměru kružnice $r$, po níž pohyb probíhá.
Uvážíme-li, že se za dobu $\Delta t$ bod přemístil z místa A do místa B (viz obrázek), lze úhel, který průvodiče v jednotlivých pozicích svírají vyjádřit jako
\begin{equation} \beta={\normalsize\frac{s}{r}}\:\mbox{,}\label{eq:rce1} \end{equation}kde $s$ představuje délku oblouku kružnice mezi těmito místy. Úhel $\beta$ označujeme jako úhlovou dráhu a vyjadřujeme ji v radiánech.
Na základě analogie s rovnoměrným přímočarým pohybem ($v=\frac{s}{t}$), lze i v případě rovnoměrného pohybu po kružnici definovat úhlovou rychlost $\vec{\omega}$ vztahem
\begin{equation} \omega=\frac{\Delta\beta}{\Delta t}\,\mbox{.}\label{eq:rce2} \end{equation}Rovnoměrný pohyb po kružnici je pohyb periodický. Průvodič se vždy do stejného místa vrátí po opsání úhlu $\beta = 2\pi$ za stejnou dobu $T$ - periodu. Převrácenou hodnotu $f=\frac{1}{T}$ označujeme jako frekvenci. Pro $\Delta\beta=2\pi$ a $\Delta t=T$ dostáváme ze \eqref{eq:rce2} vztah pro úhlovou rychlost
\begin{equation} \omega=\frac{2\pi}{T}=2\pi f\mbox{.}\label{eq:rce3} \end{equation}Jestliže za dobu $\Delta t$ opíše průvodič $\vec{r}$ úhel $\Delta\beta$, je dráha, kterou bod urazil podle \eqref{eq:rce1} rovna $\Delta s=r\Delta\beta$. Velikost obvodové rychlosti $\vec{v}$ rovnoměrně se pohybujícího bodu na kružnici o poloměru $r$ lze vyjádřit jako
$$v=\frac{\Delta s}{\Delta t}=\frac{r\Delta\beta}{\Delta t}=r\frac{\Delta\beta}{\Delta t}=r\omega\mbox{.}$$
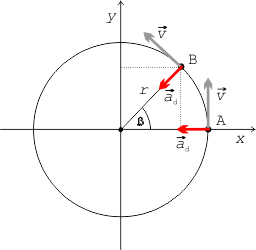
Jelikož se během pohybu mění směr okamžité rychlosti, můžeme tak stanovit velikost dostředivého zrychlení $\vec{a}_{\rm{d}}$, které směřuje vždy do středu trajektorie. Pro změnu rychlosti při přemístění z místa A do místa B platí $\Delta\vec{v}=\vec{v}_{\rm{B}}-\vec{v}_{\rm{A}}$. Vektory $\vec{v}_{\rm{A}}$ a $\vec{v}_{\rm{B}}$ spolu taktéž svírají úhel $\Delta\beta$ při přemístění do společného počátku (vektor okamžité rychlosti má vždy směr tečny k trajektorii). Úhel $\Delta\beta$ pak lze vyjádřit $\Delta\beta=|\Delta\vec{v}|/v=\Delta s/r$. Dosazením do obecného vztahu
$$\vec{a}=\frac{\Delta\vec{v}}{\Delta t}$$dostáváme pro velikost dostředivého zrychlení
\begin{equation} a_{\rm{d}}=\frac{|\Delta\vec{v}|}{\Delta t}=\frac{\Delta s\,v}{\Delta t\,r}=\frac{v^{2}}{r}=\omega^{2}r\,\mbox{.}\label{eq:rce4} \end{equation}Videoanalýza
Nepochybně existuje řada způsobů, jak vhodně demonstrovat rovnoměrný pohyb po kružnici. Jako jedno z možných řešení se nabízí využití gramofonu.
Pomůcky
Gramofon, kamera, barevná lepící páska, nůžky, vhodné měřidlo, software pro analýzu a zpracování videa.

Provedení
- K demonstraci rovnoměrného pohybu po kružnici je možné využít gramofon, na jehož talíř ve vhodné vzdálenosti od středu otáčení umístíme značku vyrobenou z kontrastní lepící pásky. V tomto případě byla programem TRACKER tato vzdálenost změřena $r\approx 8\:\rm{cm}$.
- Před samotným analyzováním je zapotřebí provést změření šířky význačného pruhu talíře gramofonu. Tuto hodnotu lze využít jako kalibrační vzdálenost ve videu, v našem případě $d=2,0\:\rm{cm}$.
- Aplikací filtrů lze docílit záměrného zanechávání stopy pohybu vybraného bodu.
- Využitím vhodných voleb lze nastavit zobrazování vektorů okamžité rychlosti a zrychlení. Vektor okamžité rychlosti by měl mít směr tečny a vektor dostředivého zrychlení by měl směřovat do středu trajektorie.
- Pro ukázku souvislostí mezi pohybem po kružnici a mechanickým kmitáním zobrazíme současně dva grafy závislostí $x(t)$ a $y(t)$ nebo $v_{\rm{x}}(t)$ a $v_{\rm{y}}(t)$.
Vyhodnocení
- Z videa je patrné, že se bod po kruhové trajektorii pohybuje rovnoměrně – stopa pohybu se pravidelně objevuje. To dokazuje i graf $v(t)$, který mírně fluktuuje kolem hodnoty $v=0,27\:\rm{m\cdot s^{-1}}$.
- V případě zakreslení vektorů okamžité rychlosti a dostředivého zrychlení dostáváme správné výsledky – vektor okamžité rychlosti má vždy směr tečny a vektor dostředivého zrychlení směřuje do středu trajektorie, v tomto případě k ose otáčení gramofonu.
- Zajímavé výsledky lze získat při zobrazení závilostí
$x(t)$
a
$y(t)$.
Jednotlivé složky (průměty do souřadnicových os) jsou zakresleny harmonickými funkcemi, což je jistá analogie s mechanickým kmitáním – okamžitá výchylka mechanického oscilátoru je reprezentována hodnotou y-souřadnice. V případě, že je jedna ze složek nulová, je druhá maximální – dosahuje amplitudy a naopak. Mezi průběhy složek tak vzniká fázový rozdíl
$\Delta\varphi=\pi/2$.
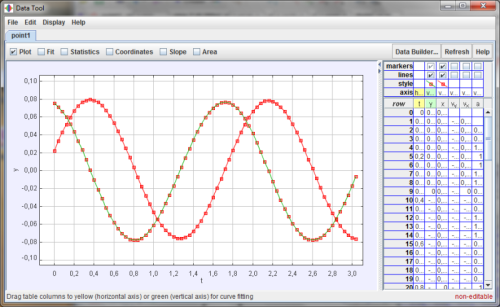 Závislost souřadnic na čase.
Závislost souřadnic na čase. - Jelikož je velikost obvodové rychlosti konstantní v dané vzdálenosti od osy otáčení, bude na základě \eqref{eq:rce4} platit totéž i pro úhlovou rychlost.
- Pro ověření správnosti získaných výsledků můžeme porovnat velikost naměřené úhlové rychlosti $\vec{\omega}$ s teoretickou úhlovou rychlostí $\vec{\omega}_{\rm{t}}$, kterou lze získat ze \eqref{eq:rce3} a ze znalosti počtu otáček za minutu pro LP desku, např. z Lit(2), konkrétně $33\:1/3\,\rm{rpm}$ (rpm – otáčky za minutu). Pro $\vec{\omega}_{\rm{t}}$ dostáváme $\omega_{\rm{t}}=3,49\:\rm{rad\cdot s^{-1}}$, pro $\vec{\omega}$ z videoanalýzy $\omega=3,50\:\rm{rad\cdot s^{-1}}$. Relativní chyba $\delta_{\rm{\omega}}=0,29\,\%$.
Použitá literatura a zdroje
- BEDNAŘÍK, Milan a Miroslava ŠIROKÁ. Fyzika pro gymnázia. 4. vyd., dotisk. Praha: Prometheus, 2011, 288 s. ISBN 978-807-1963-820.
- Gramofonová deska. Wikipedie. Dostupné z: http://cs.wikipedia.org/wiki/Gramofonová_deska.





