Matematické kyvadlo se zarážkou

Střední škola, pokročilí

Vysoká škola

27. 3. 2012, 0:15

15. 12. 2012, 17:26

Zdeněk Pucholt

Cíl úlohy

Určit umístění zarážky od bodu závěsu matematického kyvadla ze znalosti celkové doby kmitu a nezkrácené délky závěsu.

Fyzikální princip

Periodu kmitání matematického kyvadla lze ovlivnit změnou délky závěsu $l$, přemístěním kyvadla do místa s výrazně odlišnou hodnotou tíhového zrychlení $g$ nebo umístěním vhodné zarážky svisle pod bod závěsu ve vzdálenosti $\Delta l$.

Využitím poslední možnosti lze experimentálně pomocí videoanalýzy ověřit velikost vzdálenosti $\Delta l$ ze znalosti doby kmitu kyvadla $T$ a délky celého závěsu $l$.

Pro vzdálenost $\Delta l$ zřejmě platí

\begin{equation} \Delta l=l-l_0\:\mbox{,}\label{eq:rce1} \end{equation}

kde $l_0$ označuje vzdálenost mezi zarážkou a těžištěm kuličky.

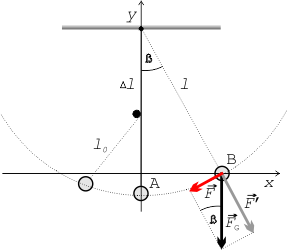
Matematické kyvadlo se zarážkou – nákres možné situace.

Pro teoretické určení periody tohoto kyvadla vycházíme z předpokladu možného rozdělení pohybu na dvě nezávislá kyvadla, jedno o délce závěsu $l$, druhé o délce $l_0$. Jelikož každé dílčí kyvadlo vykoná pouze $1/2$ periody, potom platí

$$T_{\rm {celk}}=T+T_0\:\mbox{,}$$

kde

$$T=\pi\sqrt{\frac{l}{g}}\:\mbox{,}$$ $$T_0=\pi\sqrt{\frac{l_0}{g}}\:\mbox{.}$$

Celková perioda kyvadla tedy bude

$$T_{\rm{celk}}=\pi\sqrt{\frac{l}{g}}+\pi\sqrt{\frac{l_0}{g}}\:\mbox{,}$$

odkud pro vzdálenost $l_0$ dostáváme

\begin{equation} l_0=\frac{(T_{\rm{celk}}-\pi\sqrt{\frac{l}{g}})^2g}{\pi^2}\:\mbox{.}\label{eq:rce2} \end{equation}

Videoanalýza

Pomocí videoanalýzy pohybu kyvadla lze poměrně přesně stanovit velikost jeho periody. S využitím \eqref{eq:rce2} a změřením délky závěsu $l$ můžeme určit umístění zarážky.

Pomůcky

Kulička s háčkem, nit, nůžky, závěs na zdi pro zavěšení matematického kyvadla, laboratorní stojan, držáky na stojan, zarážka, kamera, software pro analýzu a zpracování videa.

Využití kuličky a nitě k vytvoření matematického kyvadla.

Provedení

Před samotným analyzováním je zapotřebí provést změření průměru použité kuličky, v našem případě $d=25,3\:\rm{mm}$. Velikost průměru kuličky lze využít jako kalibrační vzdálenost ve videu.
Dále je nutné provést změření délky nezkráceného závěsu $l$ (vzdálenost bodu uchycení závěsu – těžiště kuličky), v našem případě $l=1,003\:\rm{m}$.
Svisle pod bod závěsu kyvadla umístíme stojan se zarážkou.
Kameru umístíme tak, aby v záběru bylo celé kyvadlo – od bodu závěsu po kuličku.
Výstupem videoanalýzy je komplexní video obsahující graf závislosti x-souřadnice na čase $x(t)$.
Matematické kyvadlo – matematické kyvadlo se zarážkou.

Vyhodnocení

Původní nastavená metrová délka závěsu se změnila vlivem tíhy kuličky a háčku.
Pomocí videoanalyzačního programu určíme periodu, v našem případě $T_{\rm{celk}}=1,65\:\rm{s}$. Pak pro $l_0$ na základě \eqref{eq:rce2} dostáváme $l_0=0,41\:\rm{m}$. Podle \eqref{eq:rce1} tak pro vzdálenost zarážky od bodu závěsu platí $\Delta l\approx 0,59\:\rm{m}$.
Při kontrolním měření pomocí analyzačního programu dostáváme pro vzdálenost $\Delta l_{\rm t}=0,60\:\rm{m}$, což se nepatrně liší od experimentálně stanovené hodnoty z doby kmitu kyvadla $\Delta l\approx 0,59\:\rm{m}$. Pro relativní chybu měření dostáváme $\delta_{\rm{\Delta l}}=1,7\,%$.
Z naměřených hodnot je zřejmé, že díky poměrně přesnému určení doby kmitu kyvadla lze stanovit umístění zarážky od bodu závěsu. Tato hodnota je v rámci naší přesnosti téměř shodná s hodnotou, kterou lze naměřit ve videoanalyzačním programu.

Použitá literatura a zdroje

KALUŽAY, Josef a Michal ZEMAN. 500 riešených úloh z fyziky. 1. vyd. Bratislava: ALFA, 1973, 276 s. 63-095-73.
LEPIL, Oldřich. Fyzika pro gymnázia: Mechanické kmitání a vlnění. 3. přeprac. vyd. Praha: Prometheus, 2001, 129 s. ISBN 80-719-6216-3.

Diskuze (0)

Fotogalerie (4)

Videogalerie (1)

Přiložené soubory (1)